Beim Übergang zwischen den Schichten eines KNN ist der Einsatz von linearen Funktionen nicht sinnvoll, da die Kombination linearer Funktionen wieder eine lineare Funktion ergibt. In einem solchen Fall ließen sich die beiden Schichten durch eine einzelne ersetzen.
Wir brauchen daher als Übergangsfunktion etwas anderes. Plausibel sind folgende Anforderungen an die Funktion:
- Sie sollte nicht-linear sein
- Sie sollte einen Wertebereich zwischen 0 und 1 haben – keine Verstärkung oder etwa sogar Vorzeichenumkehr
- Sie sollte monoton steigend sein – stärkerer Input führt zu stärkerem Output
- Sie sollte einfach zu differenzieren sein – dadurch wird einfache Backpropagation möglich
Sigmoidale Funktionen
Dies führt schnell auf eine S-förmige Gestalt der Funktion, woher die Bezeichnung Sigmoidale Funktion oder Sigmoid-Funktion stammt. Am häufigsten wird die Logistische Funktion eingesetzt:
![]()
Neben ihrem schönen S-förmigen Verlauf ist ihre Ableitung recht einfach:
![]()
Hat man also ![]() , berechnet, so muss man für die Berechnung von
, berechnet, so muss man für die Berechnung von ![]() nur noch multiplizieren.
nur noch multiplizieren.
ReLU-Funktionen
Eine weitere Funktionsart, die häufig als Transferfunktion zum Einsatz kommt, sind die ReLU-Funktionen. ReLU steht für Rectified Linar Unit, wobei Rectifier für Gleichrichter steht. Die Funktion
![]()
wird als Leaky-ReLU-Funktion bezeichnet bezeichnet. Für Werte größer 0 reicht sie den Wert einfach durch, Werte kleiner 0 werden mit 0,2 multipliziert und somit verkleinert.
Implementierung
Die Implementierung mit NumPy ist wieder simpel:
def sigma(x):
return 1 / (1 + np.exp(-x))
def sigma_1(x):
return sigma(x) * (1- sigma(x))
def leaky_relu(x):
return np.maximum(0.2 * x,x)
def leaky_relu_1(x):
return np.array([0.2 if x < 0 else 1 for x in x] )
Graphische Darstellung
plt.figure( figsize=(12, 4))
def do_plot(nr, name, f,f_1):
plt.subplot(1,2,1)
plt.title('Die Funktion  und ihre Ableitung')
plt.xlabel('
und ihre Ableitung')
plt.xlabel('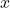 ')
plt.ylabel('
')
plt.ylabel('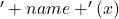 ')
plt.grid(True)
plt.plot(x,f(x))
plt.plot(x,f_1(x))
x = np.linspace(-10,10,200)
do_plot(1,'\sigma',sigma,sigma_1)
plt.subplot(1,2,2)
plt.title('Die Leaky-ReLU-Funktion und ihre Ableitung')
plt.xlabel('
')
plt.grid(True)
plt.plot(x,f(x))
plt.plot(x,f_1(x))
x = np.linspace(-10,10,200)
do_plot(1,'\sigma',sigma,sigma_1)
plt.subplot(1,2,2)
plt.title('Die Leaky-ReLU-Funktion und ihre Ableitung')
plt.xlabel('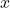 ')
plt.ylabel('
')
plt.ylabel('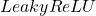 ')
plt.grid(True)
plt.plot(x,leaky_relu(x))
plt.plot([-10,0],[-0.2,-.2],color='Orange')
plt.plot([0,10],[1,1],color='Orange')
plt.show()
plt.show()
')
plt.grid(True)
plt.plot(x,leaky_relu(x))
plt.plot([-10,0],[-0.2,-.2],color='Orange')
plt.plot([0,10],[1,1],color='Orange')
plt.show()
plt.show()
Berechnung der Ableitung der Logistischen Funktion
Die logistische Funktion lautet:
![]()
![]()
mit zweimaliger Anwendung der Kettenregel, und andererseits
![]()
Die beiden rechten Seiten stimmen überein, also gilt
![]()
Man muss zur Berechnung der Ableitung von ![]() wieder nur
wieder nur ![]() selbst berechnen.
selbst berechnen.

